Benchmarking Rust code with Criterion.rs

Introduction

Benchmarking is a method of systematically assessing a program for performance. This process is a valuable component of regression testing because it helps you compare changes and improvements to your code. The systems programming language Rust offers many statistically rigorous analysis techniques, such as the Criterion crate, which is a popular tool used for benchmarking in Rust. In this article, we’ll go into more detail on how to use Criterion to compare various Rust functions to solve a problem from Project Euler.

About Criterion

Criterion is a benchmarking crate that specializes in statistically rigorous analysis techniques, as well as generating useful and attractive charts using gnuplot. The primary goals of Criterion are to measure the performance of code, prevent performance regressions, and accurately measure optimizations.

Example

To understand how to use Criterion for benchmarking, let’s re-use an example from a previous article where we learned how to implement parallel processing in Rust. In that article we explored how to parallelize a commutative loop. This time, let’s compare the parallelized function to a function that solves the problem with an arithmetic series. The problem:

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 1000000.

Setup steps

The code used in this article can be found at https://github.com/AshwinSundar/Criterion-Benchmarking. Let’s start by creating a new Rust project in an empty folder called Criterion_Benchmarking. cd into the folder and type cargo init.

Terminal

❯ cargo init
     Created binary (application) package

1. Add Criterion to dev-dependencies

$PROJECT/Cargo.toml

[dev-dependencies]
criterion = {version = "0.3", features = ["html_reports"]}

[[bench]]
name = "euler1_benchmark"
harness = false

First, navigate to the Rust manifest file Cargo.toml and create a dev-dependencies section. Adding Criterion to this section ensures that the benchmarking crate is only included during testing, and not in production builds. Let’s also disable the default benchmarking harness libtest by setting harness=false, that way the compiler invokes the Criterion benchmarking harness instead.

2. Create benchmark file

$PROJECT/benches/euler1_benchmark.rs

use criterion::{black_box, criterion_group, criterion_main, Criterion};
// use lib::euler1; // function to profile

pub fn criterion_benchmark(c: &mut Criterion) {
// c.bench_function("euler1", |b| b.iter(|| euler1(black_box(input))));
}

criterion_group!(benches, criterion_benchmark);
criterion_main!(benches);

Next, create a benchmark file at $PROJECT/benches/euler1_benchmark.rs. This file will import our function, run a benchmark, and then output the results to the console using a macro. We’ll leave a couple placeholders for now and revisit this file once we’ve built the functions to benchmark.

3. Create library file

$PROJECT/src/lib.rs

#[inline]
pub fn euler1_simple() {
    // For-loop solution
}

#[inline]
pub fn euler1_par() {
    // Parallelized solution
}

#[inline]
pub fn euler1_series() {
    // Arithmetic series solution
}

Finally, due to implementation constraints within Criterion, we need to create a library file to host our functions at src/lib.rs and declare our functions as public, so that we can import the functions into euler1_benchmark.rs. The #[inline] attribute above the function helps reduce execution time slightly and improves the accuracy of the benchmarking process.

Now that we’ve written some boilerplate code for the benchmark, let’s return to the actual problem and compare a few possible solutions.

Solutions

If you’re interested in the details of each solution, read this section. Otherwise, you can skip to the Creating Benchmarks section. Just know that the three solutions are, in order of least to most efficient, a simple for-loop, a parallelized for-loop, and an arithmetic series.

To reiterate the problem:

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 1000000.

Solution 1: For-loop

$PROJECT/src/lib.rs

#[inline]
pub fn euler1_simple(input: i64) -> i64 {
    let mut sum: i64 = 0;
    for i in 1..input {
        if i % 3 == 0 || i % 5 == 0 {
            sum += i as i64;
        }
    }
    sum

}

A simple brute-force solution is to iterate on every number in the range and determine if it’s divisible by either 3 or 5. This solution will give us a good baseline to compare the other solutions to.

Solution 2: Parallelized for-loop

$PROJECT/src/lib.rs

#[inline]
pub fn euler1_par(input: i64) -> i64 {
    use std::thread;

    let threads = thread::available_parallelism().unwrap().get() as f64;
    let input = input as f64;
    let mut handles: Vec<JoinHandle<i64>> = vec![];

    for t in 1..=(threads as i32) {
        let t = t as f64;
        let upper_bound = (input * (t / threads)) as i32;
        let lower_bound = (input * (t - 1f64) / threads) as i32;

        handles.push(thread::spawn(move || {
            let mut sum: i64 = 0;
            for i in lower_bound..upper_bound {
                if i % 3 == 0 || i % 5 == 0 {
                    sum += i as i64;
                }
            }
            sum
        }));
    }

    let mut sum = 0;

    for h in handles {
        sum += h.join().unwrap();
    }
    sum

}

In a previous article, we started to explore parallelization using std::thread, a library for distributing program processing to OS threads. We stopped at two threads in that article, so in this example I’ve expanded the function to accomodate all available system threads.

Let’s step through this code piece by piece.

    use std::thread;

    let threads = thread::available_parallelism().unwrap().get() as f64;
    let input = input as f64;
    let mut handles: Vec<JoinHandle<i64>> = vec![];

First, we need to import the native parallelism module std::thread and determine how many OS threads are available on the system using std::thread::available_parallelism().

    for t in 1..=(threads as i32) {
        let t = t as f64;
        let upper_bound = (input * (t / threads)) as i32;
        let lower_bound = (input * (t - 1f64) / threads) as i32;

        handles.push(thread::spawn(move || {
            let mut sum: i64 = 0;
            for i in lower_bound..upper_bound {
                if i % 3 == 0 || i % 5 == 0 {
                    sum += i as i64;
                }
            }
            sum
        }));
    }

Next, we set up all our threads using thread::spawn, and pass in a closure containing the same calculation as euler1_simple. The trick to this code is that the range of elements being iterated upon must be split up and processed. The range for each handle to process is computed in upper_bound and lower_bound. As each handle completes, its output is pushed into a vector of handles.

    let mut sum = 0;

    for h in handles {
        sum += h.join().unwrap();
    }
    sum
}

Since the calculations in each subset of the range are independent of each other, the final outputs are commutative and can be summed up with sum += h.join().unwrap();

Solution 3: Arithmetic Series

The sum of the multiples of 3 or 5 is a composite arithmetic series. An arithmetic series is the sum of a sequence of numbers where each subsequent term can be calculated by adding a constant \(d\) to the last term. For example, for the sequence \(2,5,8,...a_n\), for \(a_1=2\), \(d=3\), and can be represented as:

Naturally, it follows that the sum of this sequence is:

Cleverly, the series formula is derived by rewriting this sum in another way, with respect to the last value in the sequence \(a_n\):

Adding these two formulas together causes all terms involving \(d\) to cancel out, and we’re left with \(2S_n = n(a_1 + a_n)\), which simplifies to \(S_n = \frac{n}{2}(a_1 + a_n)\).

In the special case where each number in the sequence is a multiple of the first (e.g. 3, 6, 9, 12), then \(a_n = n * a_1\), and the formula can be written as \(S_n = \frac{n}{2}(a_1 + n * a_1)\), which simplifies to:

This is the formula we’ll implement in the code below.

$PROJECT/src/lib.rs

#[inline]
pub fn euler1_series(input: i64) -> i64 {
    let val = input - 1;
    let n_3 = val / 3;
    let n_5 = val / 5;
    let n_15 = val / 15;

    let sum_three = 3 * n_3 * (1 + n_3) / 2;
    let sum_five = 5 * n_5 * (1 + n_5) / 2;
    let sum_fifteen = 15 * n_15 * (1 + n_15) / 2;

    sum_three + sum_five - sum_fifteen
}

Recall that the original problem asks to calculate the sum of the multiples below input, which is why we first declare let val = input - 1;. This was implicitly handled in the for loops in the previous two solutions, because the upper bound of the range iterator is exclusive. Next, we find the number of terms n by using the fact that the integer type in Rust implements division in such a way that the result is floored, so that the answers remains an integer. Finally, we implement the series formula for multiples of 3 and multiples of 5, add the results, and subtract the sum of the multiples of 15, because it is the least common multiple of 3 and 5.

Creating Benchmarks

Replace the code in benches/euler1_benchmark.rs with:

$PROJECT/benches/euler1_benchmark.rs

use criterion::{black_box, criterion_group, criterion_main, Criterion};
use criterion_benchmarking::{euler1_par, euler1_series, euler1_simple};

fn criterion_benchmark(c: &mut Criterion) {
    let input = 1000000;
    c.bench_function("simple", |b| b.iter(|| euler1_simple(black_box(input))));
    c.bench_function("parallel", |b| b.iter(|| euler1_par(black_box(input))));
    c.bench_function("series", |b| b.iter(|| euler1_series(black_box(input))));
}

criterion_group!(benches, criterion_benchmark);
criterion_main!(benches);

In the above code, .bench_function defines a benchmark with a name and a closure. The name must be unique among the benchmarks in the project. The closure accepts one argument, Bencher, which is a Timer struct used to iterate a benchmarked function and measure the runtime. black_box is a function that prevents the Rust compiler from pre-optimizing the function prior to runtime, which can result in a quicker benchmark time than real-world use cases. criterion_group!(...) and criterion_main!(...) are macros, which together generate a benchmark group and a main function that executes the benchmarks. This is also why the benchmark is conducted in a separate file from main.rs, which already defines its own main() function.

To run the benchmark, type cargo bench in the terminal. After several seconds, you should see an output like this:

> cargo bench
Benchmarking simple: Warming up for 3.0000 s
simple                  time:   [1.1540 ms 1.1564 ms 1.1589 ms]
Found 2 outliers among 100 measurements (2.00%)
  1 (1.00%) high mild
  1 (1.00%) high severe
Benchmarking parallel: Warming up for 3.0000 s
parallel                time:   [224.43 us 227.90 us 231.96 us]
Found 10 outliers among 100 measurements (10.00%)
  5 (5.00%) high mild
  5 (5.00%) high severe
Benchmarking series: Warming up for 3.0000 s
series                  time:   [2.4586 ns 2.4645 ns 2.4708 ns]
Found 1 outliers among 100 measurements (1.00%)
  1 (1.00%) high mild

The time array represents a 95% confidence interval, where the mean execution time is the second value in the array. Outliers are determined using a modified version of Tukey’s method.

A more consumable version of this information is automatically generated and is available in $PROJECT/target/criterion/{benchmark-name}/report/index.html.

Under the Hood

Before we compare the charts for each function, let’s briefly explore what Criterion is doing behind the scenes. The first step of the process is warm-up, which involves running the function repeatedly for a short period of time in order to allow the CPU and OS caches to adapt to the new load.

Second, after the warm-up process is complete, measurements are taken by repeatedly running the function under examination.

Third, the samples are analyzed and the results are compiled into useful statistics for the user. This involves custom outlier analysis and linear regression analysis.

Finally, the current run is compared to the previous run to determine if any statistically significant change has occurred, which is reported to the user.

More details about the analysis process can be found at https://bheisler.github.io/criterion.rs/book/analysis.html.

Comparing Functions

Let’s look at the reports for each function.

euler1_simple

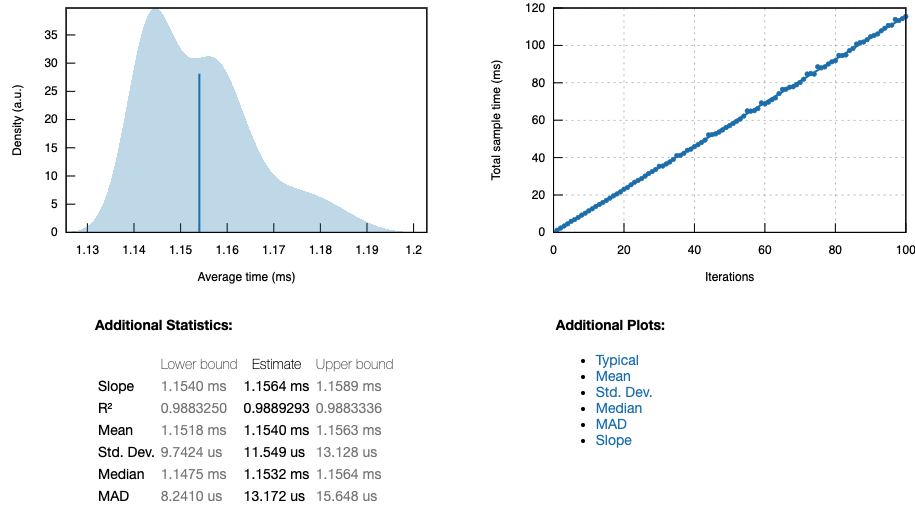
euler1_par

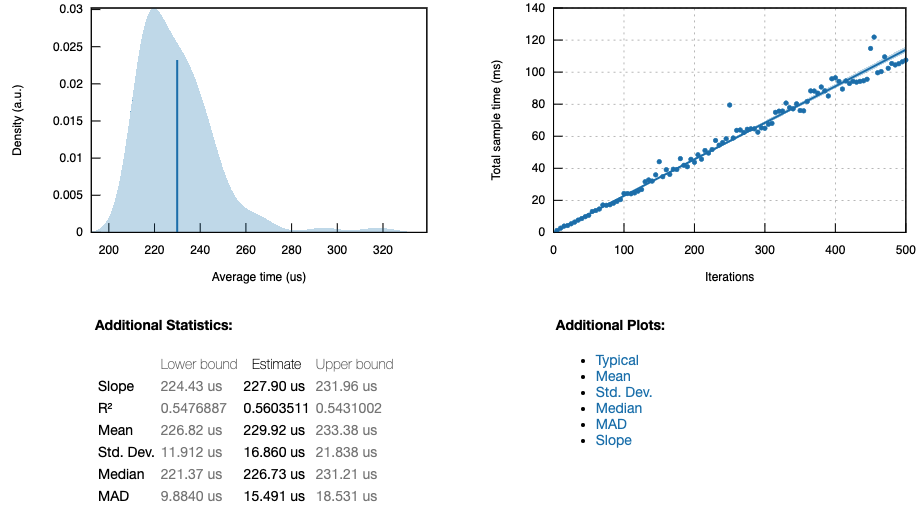
euler1_series

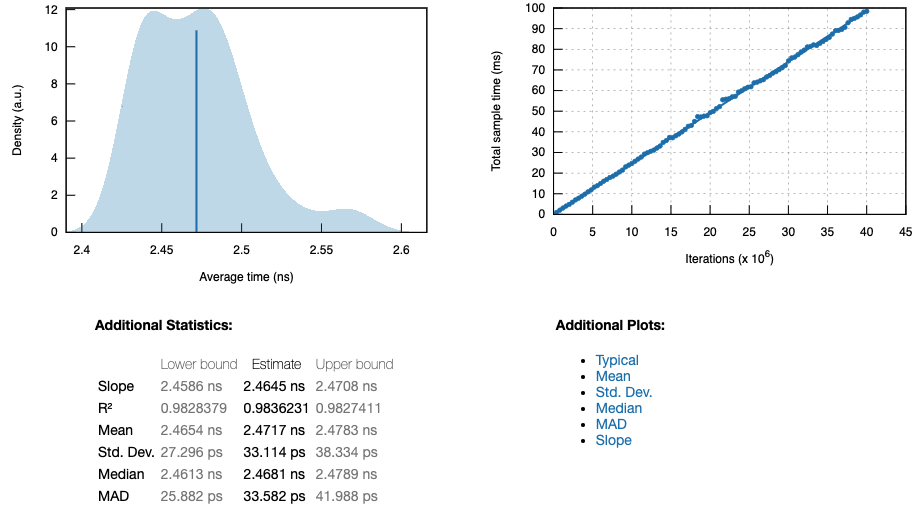
The top left plot in each report is a probability density function, which depicts the average time per iteration of the function. The blue bar represents the overall mean. The shaded region represents the probability that execution of this function will take a particular amount of time, while integrating the area between two times will provide the probability that the function will execute within that range of time. The top right plot is the linear regression for the function. Each iteration is plotted in order and the y-axis represents cumulative time to execute all iterations up to that point. The slope of this line is given under Additional Statistics.

R² and standard deviation are also useful statistics to look at. In the context of the benchmarking process, a low R² means in statistical terms that a significant amount of the variability between each iteration isn’t attributable to differences in the function itself. However, we know that every time the function executes, the exact same code is executed, so what does that sentence actually mean? In this context, it means that the benchmarking process we’ve written is not behaving the same way in each iteration.

For euler1_par, this is in fact the case. I think the reason that this function in particular has a lot of variability is because it is implementing a parallelization routine, which relies on the processor to queue up tasks. How each handle is queued may vary based on the instantaneous load when each iteration is executed.

The standard deviation tells you (for a roughly normally distributed curve) that 95% of the samples landed between \(µ ± 2σ\) (mean time ± 2 standard deviations).

Advanced Features

Criterion has a lot of advanced features for the statistically inclined, two of which we’ll explore in more detail: benchmark_group and bench_with_input.

criterion::Criterion::benchmark_group

It’s apparent that the parallelized function(\(µ=227.90 us\)) is nearly 1 order of magnitude faster than the simple(\(µ=1.1564 ms\)) function, while the series function(\(µ=2.4645 ns\)) is nearly 3 orders of magnitude faster. We can generate a combined report that summarizes the performance of all three functions by associating them with each other using benchmark_group.

use criterion::{black_box, criterion_group, criterion_main, Criterion};
use criterion_benchmarking::{euler1_par, euler1_series, euler1_simple};

fn criterion_benchmark(c: &mut Criterion) {
    let input = 1000000;
    let mut group = c.benchmark_group("Euler 1");
    group.bench_function( "simple - test 1", |b| b.iter(|| euler1_simple(black_box(input))) );
    group.bench_function( "parallel - test 1" , |b| b.iter(|| euler1_par(black_box(input))));
    group.bench_function( "series - test 1", |b| b.iter(|| euler1_series(black_box(input))));
    group.finish();
}

criterion_group!(benches, criterion_benchmark);
criterion_main!(benches);

In the above code, we follow nearly the same process as individual benchmarking, except we first create and name a BenchmarkGroup using c.benchmark_group(name), which is merely an entity used to group related benchmarks for analysis and reporting. The compiled output is available at $PROJECT/target/criterion/Euler 1/report/index.html, while individual reports for each function are available at $PROJECT/target/criterion/Euler1/{benchmark-name}/report/index.html.

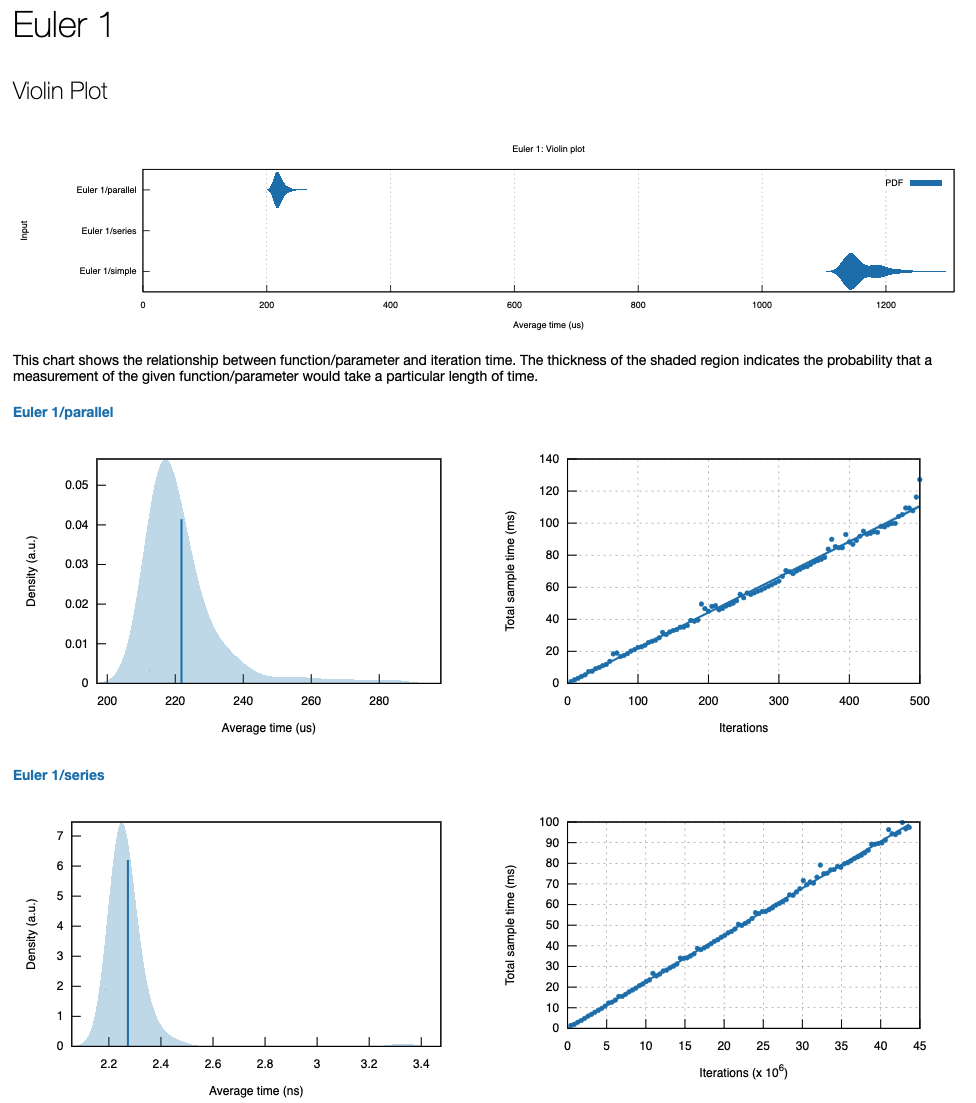
criterion::Criterion::bench_with_input

To thoroughly benchmark a function, it’s important to test it across a range of acceptable values. bench_with_input helps test a wide range of cases more effectively.

use criterion::{black_box, criterion_group, criterion_main, BenchmarkId, Criterion};
use criterion_benchmarking::{euler1_par, euler1_series, euler1_simple};

fn criterion_benchmark(c: &mut Criterion) {
    let inputs = [100, 1000, 10000, 100000, 1000000];
    let mut group = c.benchmark_group("Multiple inputs");
    for i in inputs {
        group.bench_with_input(BenchmarkId::new("euler1_simple", i), &i, |b, &i| {
            b.iter(|| euler1_simple(black_box(i)))
        });
        group.bench_with_input(BenchmarkId::new("euler1_par", i), &i, |b, &i| {
            b.iter(|| euler1_par(black_box(i)))
        });
        group.bench_with_input(BenchmarkId::new("euler1_series", i), &i, |b, &i| {
            b.iter(|| euler1_series(black_box(i)))
        });
    }
    group.finish();

}

criterion_group!(benches, criterion_benchmark);
criterion_main!(benches);

Note that we added BenchmarkId to the use declaration for Criterion. Next, we create an array of input values to assess, as well as a new BenchmarkGroup. We then iterate across the array of inputs, and call bench_with_input with a unique BenchmarkId and a closure that passes input i to the function being tested.

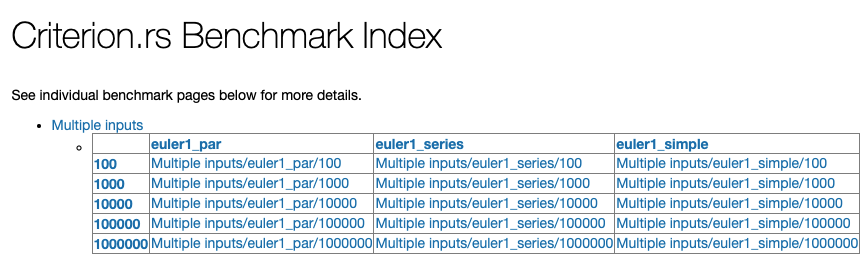
A summary of all of our reports so far is available at $PROJECT/criterion/report/index.html. The tabular format for the Multiple inputs tests is a great way to compare multiple functions across a range of inputs, as well as slice the data by two explanatory variables - the function and the input. This level of detail allows us to explore relationships between multiple explanatory variables using a concept called Response Surface Methodology. Unfortunately, Criterion is currently lacking in the abilty to generate 3-dimensional graphs needed to explore this concept in more detail.

Benchmarking across a wide range of inputs helps you find use cases that suffer from sub-optimal performance. For example, I found that euler1_simple and euler1_par take a significant amount of time to process the maximum value available in i64, ~\(9.22 * 10^{18}\), indicating that these functions should be modified to accept an integer type with a smaller number space as an input parameter.

Final Thoughts

If you write code for a living, chances are that someone else will have to reference, re-use, or adapt your code for another purpose in the future. Therefore, it’s important to be a good custodian of the code you write by considering performance and ensuring it can function as expected through the range of its intended use conditions and beyond. Benchmarking is a key tool for understanding how your code functions under the hood and making improvements in a scientific manner.

The benchmarking process is highly sensitive to the testing environment, so great care should be taken to ensure that tests are conducted in as similar environment to each other as possible, for example on the same machine with similar background loads between tests.

I have found Rust to be incredibly well-documented, among the best I’ve encountered in my career. The Criterion library is no exception, and as a result a lot of the material for this article was derived from the original documentation for Criterion.

This article was originally written for the engineering blog at DEPT®, a technology consultancy